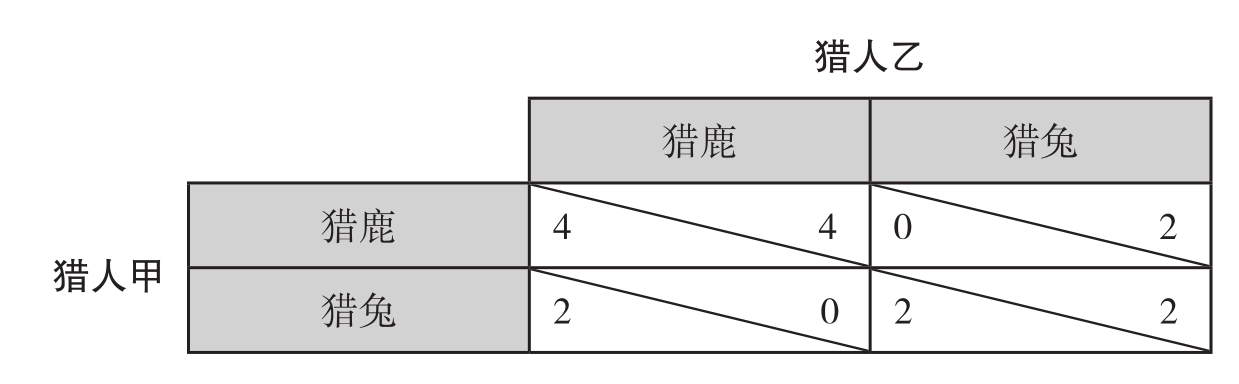
猎鹿博弈(stag hunt game)又称猎鹿模型(stag hunt model),源自法国启蒙思想家让-雅克·卢梭(Jean-Jacques Rousseau,1712—1778)的着作《论人类不平等的起源和基础》中的一个故事。两个人出去打猎,猎物为鹿和兔子。如果两个人独自去打兔子,一天下来可以打到2只兔子,如果选择去打鹿,这个时候就需要两个人共同合作才能成功打到鹿。一只鹿的价值相当于8只兔子,两个人平分以后相当于每个人打到了4只兔子。如果一个人选择打兔子,另一个人选择去打鹿,那么打鹿的人会一无所获,而选择打兔的人仍然能得到2只兔子。表17.1给出了猎鹿博弈的四种结果。
表17.1 猎鹿博弈
不难发现,在猎鹿博弈中首先有两个纯策略的纳什均衡,要么一起去打鹿,要么分头去打兔子。一个去打鹿,一个去打兔子肯定不是纳什均衡。如果出现这种情况,其中的某一方会选择与对方相同的行为:要么选择打兔子的一方跟着对方去打鹿,要么选择打鹿的一方转而选择去打兔子。这就如前面介绍的夫妻博弈一样,夫妻双方分开过年肯定不是纳什均衡,因为总会有一方调整自己的行为,选择与对方一起过年。
在猎鹿博弈中,除了两个纯策略纳什均衡以外,还有一个混合策略纳什均衡。根据上一章介绍的混合策略纳什均衡的计算方法,我们可以算出在刚才的这个猎鹿博弈中,双方各以50%的概率打鹿或打兔子是一个混合策略纳什均衡解,每个猎人的期望收益均为2只兔子。
根据刚才的计算结果,有几个问题值得我们进一步思考。
第一,两个猎人合伙打鹿一定是最优结果。但一方选择去打鹿的前提是他能够预期到对方会选择打鹿,而对方选择去打鹿的前提也是预期到另一方会去打鹿。也就是说,只有“双方都去打鹿”成为一个共同知识的前提下,最优结果才会如期出现,这也再次说明博弈中共同知识的重要性。
第二,对于每个猎人来说,选择去打兔子的收益是2只兔子,而选择去打鹿的收益要么是4只兔子要么是0。这意味着一旦选择去打鹿,就会冒着空手而归的风险。从刚才的计算得知,在混合策略纳什均衡的情况下,对方选择打鹿的概率是50%,因此选择去打鹿的期望收益也只有2只兔子。那么,对于任何一方来说,出于规避风险的考虑(在一般情况下,人总是厌恶风险的),还不如独自去打兔子。问题就在于,当双方都意识到这一点后,一起去打鹿反而变得不太可能了。
第三,为了让双方都有一个更好的结果,提前沟通就变得非常重要了。如果双方提前约定好一起去猎鹿,那么都选择猎鹿就是一个纳什均衡结果。此时,没有人愿意偏离这个结果而选择去打兔子。反之,出于规避风险的考虑,分头去打兔子反而是一个更能预期到的纳什均衡结果。我们之前已经谈到,沟通是有成本的。在这个例子中,如果沟通成本小于4只兔子,提前沟通能够提高双方总的收益水平,反之还不如分头去打兔子。
不难想象,如果两个猎人住在同一个村子里,他们出门之前会沟通约定一起去猎鹿。如果两个猎人住得非常远,要走大半天的山路才能碰到一起,那么,他们很可能就选择独自去打兔子了。从这点看,人类之所以选择居住在城市,城市的楼之所以越建越高,除了基于节约土地的考虑,更多是出于降低沟通成本的考虑。沟通和协调成本越低,人与人之间就越容易建立合作关系。