题设为A、B、C、D、E、F六只狮子（强弱从左到右依次排序）和一只绵羊。假设狮子A吃掉绵羊后就会打盹午睡，这时比A稍弱的狮子B就会趁机吃掉狮子A，接着B也会午睡，然后狮子C就会吃掉狮子B，以此类推。

那么问题来了，狮子A敢不敢吃绵羊呢？

为了简化说明，我们先给出此题的解法。该题必须采用逆向分析法，也就是从最弱的狮子F开始分析，依次前推。

假设狮子E睡着了，狮子F敢不敢吃掉狮子E？答案是肯定的，因为在狮子F的后面已经没有其他狮子，所以狮子F可以放心地吃掉午睡中的狮子E。

继续前推，既然狮子E睡着会被狮子F吃掉，那么狮子E必然不敢吃在他前面睡着的狮子D，因为它害怕吃完E后打盹被F吃掉。

再往前推，既然狮子E不敢吃掉狮子D，那么D则可以放心去吃午睡中的狮子C。依次前推，得出C不吃B，B吃A，A不吃绵羊。所以答案是狮子A不敢吃掉绵羊。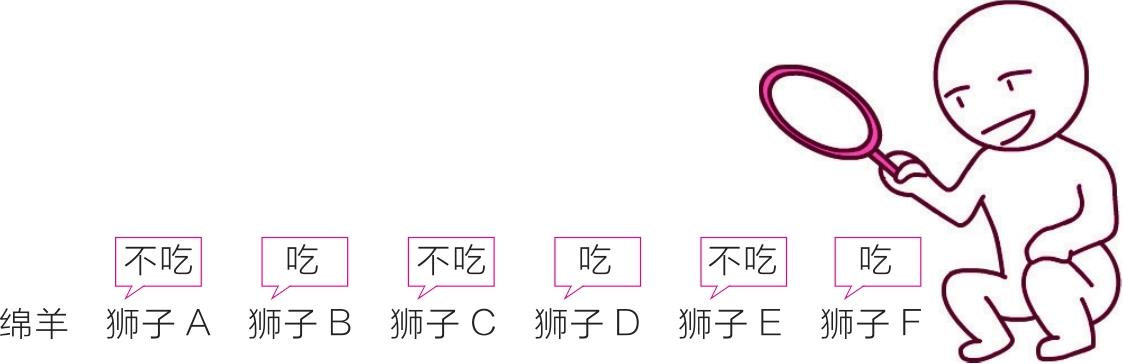

细心的人也许会发现，假如增加或减少狮子的总数，博弈的结果会完全不同。我们用下图来验证：

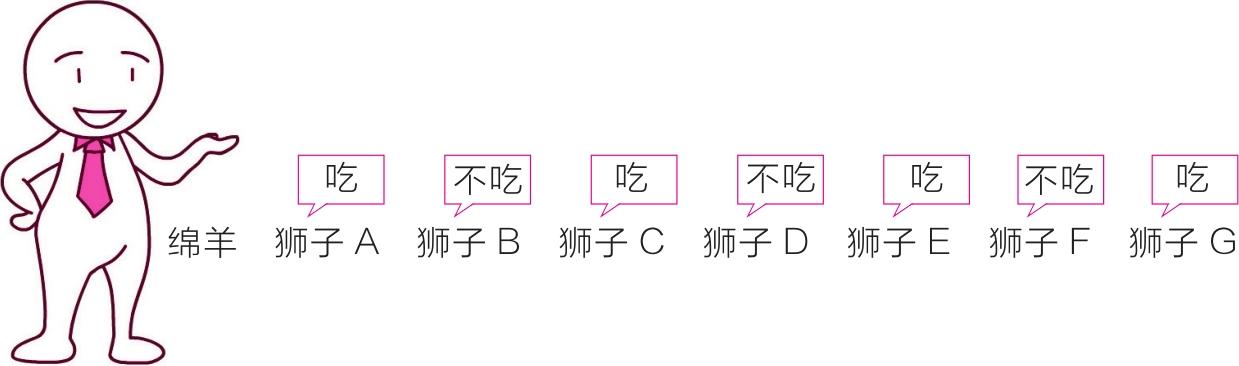
我们在狮子F的后面增加了一只狮子G，总数变成7只。用逆向分析法按照上题步骤再推一次，很容易得出结论：狮子G吃，狮子F不吃，E吃，D不吃，C吃，B不吃，A吃。这次的答案变成了狮子A敢吃掉绵羊。

对比两次博弈我们会发现，狮子A敢不敢吃绵羊取决于狮子总数的奇偶性。总数为奇数时，A敢吃掉绵羊；总数为偶数时，A则不敢吃。因此，总数为奇数和总数为偶数的狮群博弈结果形成了两个稳定的纳什均衡点。