古诺模型提出于1838年,是早期的寡头模型,也是只有两个寡头厂商的简单模型,又称“双头模型”。其结论可以推广到三个或三个以上的寡头厂商模型。
古诺的双寡头垄断模型有十分严格的条件:
①市场上只有两个寡头,生产完全相同的产品;
②为简单起见,假设生产成本为零;
③需求函数是线性的,即需求曲线是一条向右下方倾斜的直线,两个寡头分享市场;
④双方都根据对方的行动做出反应,每家寡头都通过调整产量来实现利润最大化。
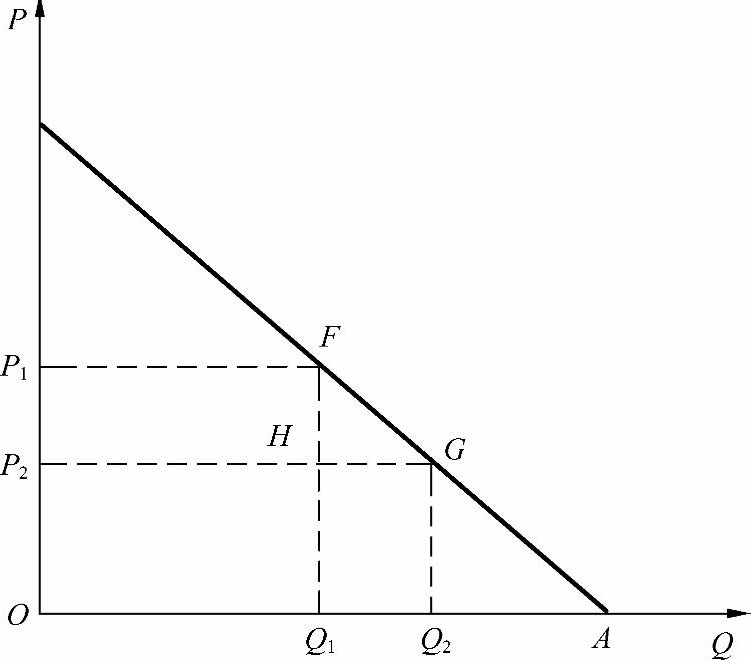
假设寡头厂商以产量为自变量、价格为因变量来推测产量,并且都假定对方不会改变原有的产量,从而求自己的最大利润。如图5.18所示,市场上只有甲、乙两个厂商生产和销售相同的产品,生产成本相同且为零,面临的市场需求曲线是向下倾斜的直线。甲、乙都准确了解市场总需求曲线,都能在已知对方产量的情况下按照利润最大化目标进行独立决策。
图5.18 古诺模型
在图5.18中,假设整个市场竞争的产量为 OA 。
第一轮,开始时甲厂商进入市场,面临的需求曲线为 OQ 1 =1/2× OA ,确定的价格为 OP 1 ,从而实现最大利润,利润量为 OQ 1 FP 1 的面积。然后乙厂商进入市场,并且认为甲厂商继续生产OQ 1 产量,从而靠甲厂商剩下的市场容量的1/2产量来实现利润最大化,产量为 O 1 Q 2 =1/4× OA ,确定的价格为 OP 2 ,利润量为 Q 1 Q 2 GH 的面积,甲厂商的利润因为价格下降减少为 OQ 1 HP 2 的面积。
第二轮,在乙厂商采取了上述行动后,甲厂商认为乙厂商会保持1/4× OA 的产量,按照 MR = MC 的原则决定产量为市场容量 OA -1/4× OA =3/4× OA 的1/2产量,即3/8× OA ,比第一轮减少3/8× OA 。然后,乙厂商认定甲厂商保持3/8× OA 的产量,乙厂商用剩下的市场容量的1/2来实现利润最大化,决定产量为1/2×5/8× OA =5/16× OA ,比第一轮增加1/16× OA 。以此类推,甲厂商的产量将逐渐减少,乙厂商的产量则逐渐增加,直到甲、乙两厂商产量相等,各自生产整个市场容量的1/3,行业产量为整个市场容量的2/3,市场达到均衡状态。
根据两个寡头厂商共同生产竞争产量的2/3的结论,可以推广到 n 个厂商的生产情况,即当达到市场均衡时,行业生产整个市场容量的 n /( n +1),每个厂商各生产1/( n +1)。