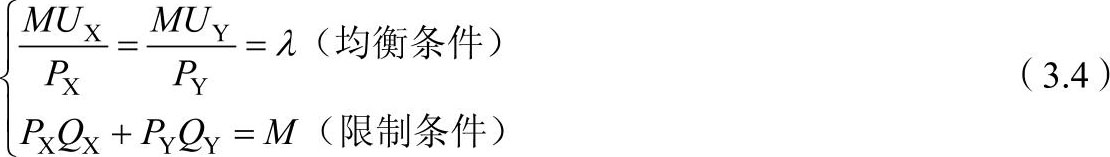假定消费者用既定的收入 I 购买两种商品X和Y， P _X 、 P _Y 分别为这两种商品的既定价格，以 Q _X 和 Q _Y 分别表示这两种商品的购买数量， MU _X 、 MU _Y 分别表示这两种商品的边际效用，同时假定消费者的收入为 M ， λ 为不变的货币的边际效用，则消费者效用最大化的均衡条件可以用公式表示为

当 MU _X / P _X < MU _Y / P _Y 时，对于消费者来说，同样的一元钱购买到商品X所得到的边际效用小于购买商品Y所得到的边际效用。这样理性的消费者就会调整这两种商品的购买数量，减少对商品X的购买量，增加对商品Y的购买量。在调整过程中，消费者减少对商品X的购买量带来的商品X的边际效用的减少量，是小于增加商品Y的购买量带来的商品Y的边际效用的增加量的，这说明消费者的总效用是增加的。当消费者将其购买组合调整到同样一元钱购买这两种商品所得到的边际效用相等，即 MU _X / P _X = MU _Y / P _Y 时，消费者就得到了最大效用。

相反，当 MU _X / P _X > MU _Y / P _Y 时，说明对于消费者来说同样的一元钱购买商品X所得到的边际效用大于购买商品Y所得到的边际效用。同理可知，消费者也会进行与前面相反的调整过程，即增加对商品X的购买，减少对商品Y的购买，直至 MU _X / P _X = MU _Y / P _Y 时消费者得到最大效用。

当 MU _X / P _X < λ 时，说明消费者用一元钱购买商品X所得到的边际效用小于所付出的一元钱的边际效用，即消费者对商品X的购买量太多了，这样理性的消费者就会减少对商品X的购买，在边际效用递减规律的作用下直至 MU _X / P _X = λ 。

当 MU _X / P _X > λ 时，说明消费者用一元钱购买商品X所得到的边际效用大于所付出的一元钱的边际效用，即消费者对商品X的购买量不足，这样理性的消费者就会增加对商品X的购买，在边际效用递减规律的作用下直至 MU _X / P _X = λ 。